Logic Circuits... or Circuit Logic

Takes in a bunch of binary inputs; returns one output; effectively it returns a binary output and as such can represent boolean expressions!

Tangent

Mr. Ibrahim keeps swapping the words “Logic Circuit” to “Circuit Logic” in the slides and IDK why but it’s a thing. Googling it, I find far more resources on the former than the latter

Boolean Expressions to Circuit Logic

Any logical expression can be described with logic gates (snatch the example from the slides)

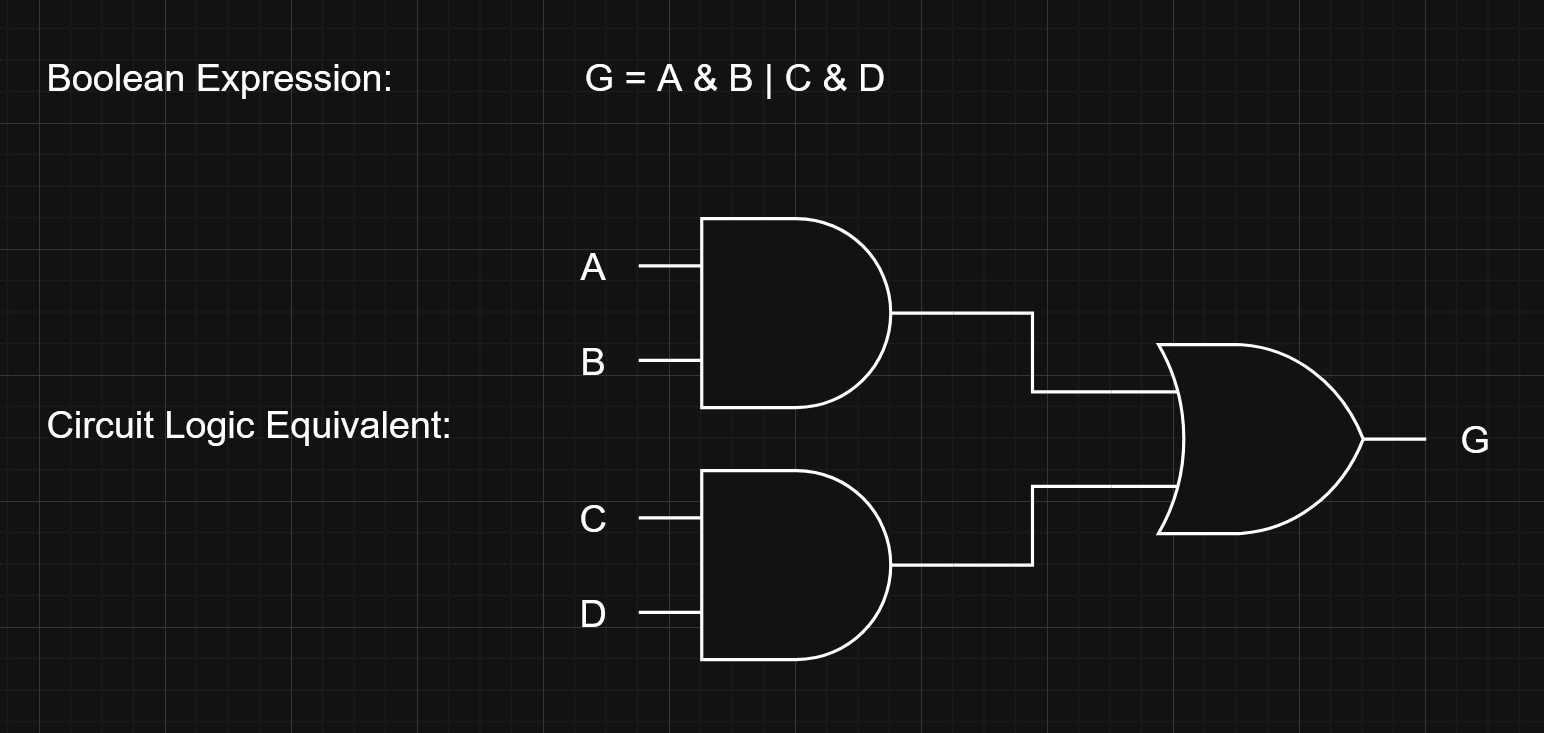
It’s useful to use “levels” based on precedence of logical operators. For instance, $(A\wedge B)\vee (C\wedge D)$ effectively represents $G$ like above in a different notation, yes, but it also emphasizes the levels via the brackets. Each bracket contains a level, and eventually these sub-levels become indivisible and only contain one logical operator which can be represented by a logic gate.

tl;dr, use the levels to guide your circuit logic representation and vice versa too!

A more complex example

Turn the following into circuit logic:

Y  = (!A and !B and !C) or
	(!A and B and C) or
	(A and B and C)

Again with the levels: each of those brackets can be one gate since the connectives within each brackets are all homogenous (there are no sublevels to be had / necessary here).

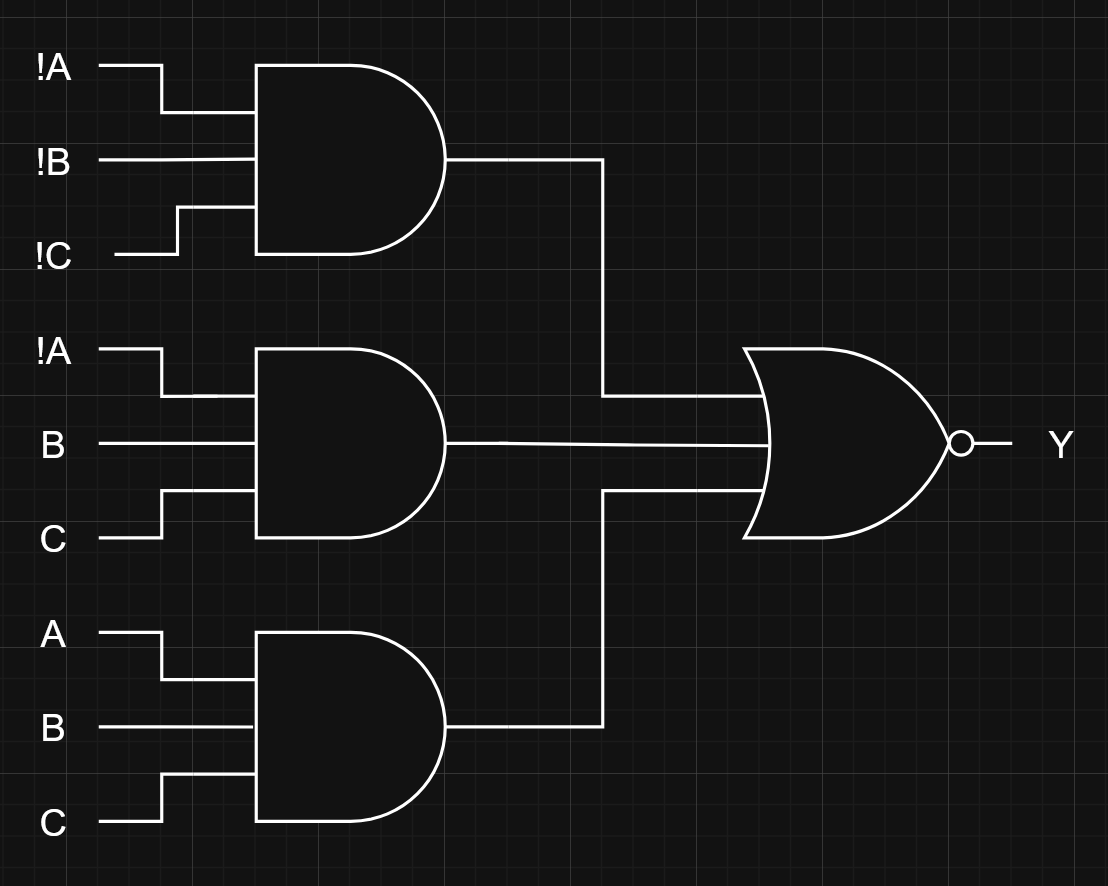
For sake of simplicity, I did not split A, B and C three times each like you should into the various places they go, because it would look like spaghetti. I am copying the slides’ approach.

However, in logic, our inputs will always be A, B, C and never $\neg A,\neg B,\neg C$; we use an inverter to pass in those negated variables into the gates as required.

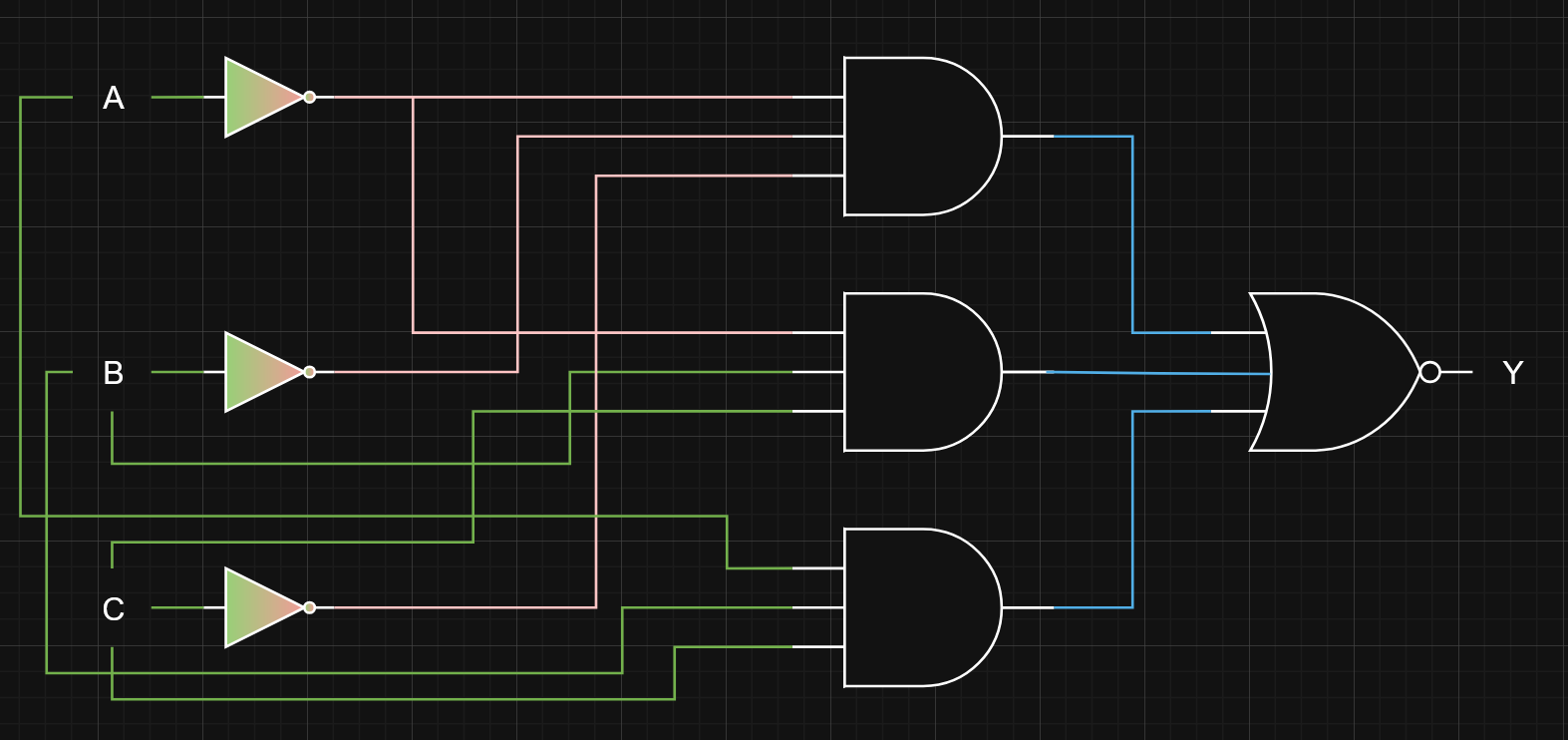
• This is what it should look like (I told you it becomes spaghetti) after using inverters. I added some colour just to show what was inverted, but no colour is required.

Vice Versa

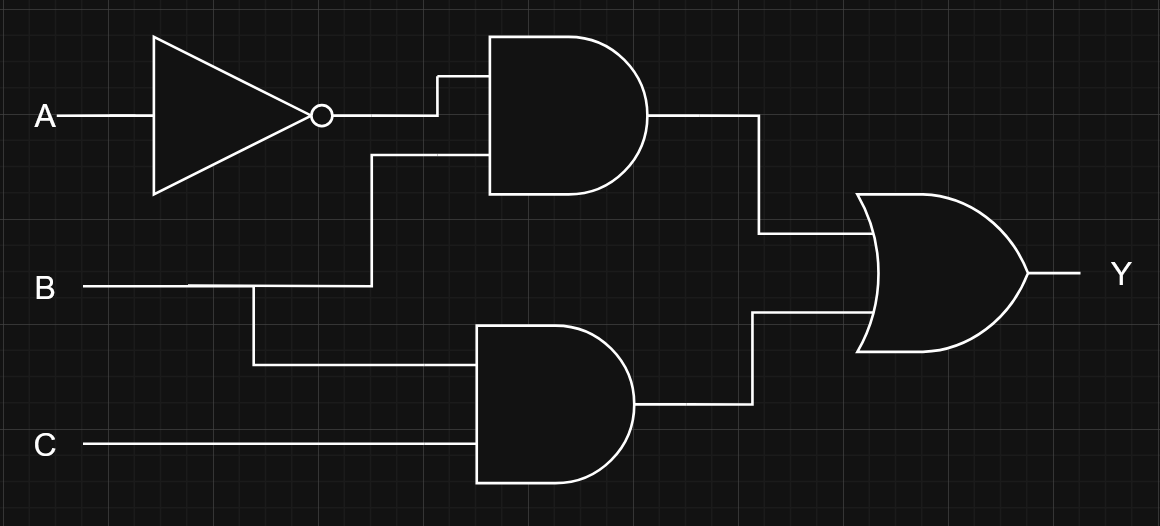
As a expression, the circuit might look like this: $(\neg A\wedge B)\vee (B\wedge C)$ Note that inversion as an operation is unary, so it can’t really have it’s own “level” unlike AND, OR, or XOR operators.

Let’s get spicier:

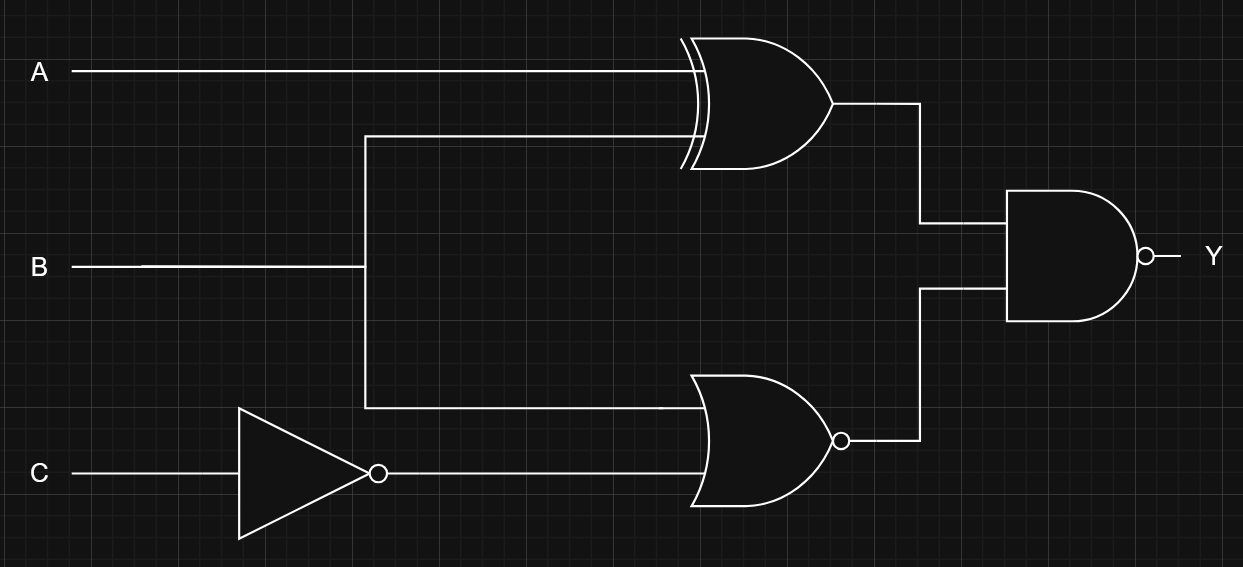
First, baby steps:

• NAND and OR are simply the AND and OR operators, but negated. Therefore, some binary inputs U and V shoved into a NAND gate could be expressed like this: $G=\neg (U\wedge V)$

Okay to build the answer, let’s do this in parts:

1. $(A\oplus B)$ for the top half with the XOR gate
   1. Refer to this note on XOR gates if the $\oplus$ notation is new / confusing.
2. $\neg (B\vee \neg C)$ for the bottom half with the NOR gate
3. $\neg ((A\oplus B)\wedge \neg (B\vee \neg C))$ for the full thing after introducing the final NAND gate.

Using the “other” notation, this expression can also be written as $\overline{(A\oplus B)\cdot \overline{B+\overline{C}}}$ which looks clean as frick ngl but also way less legible