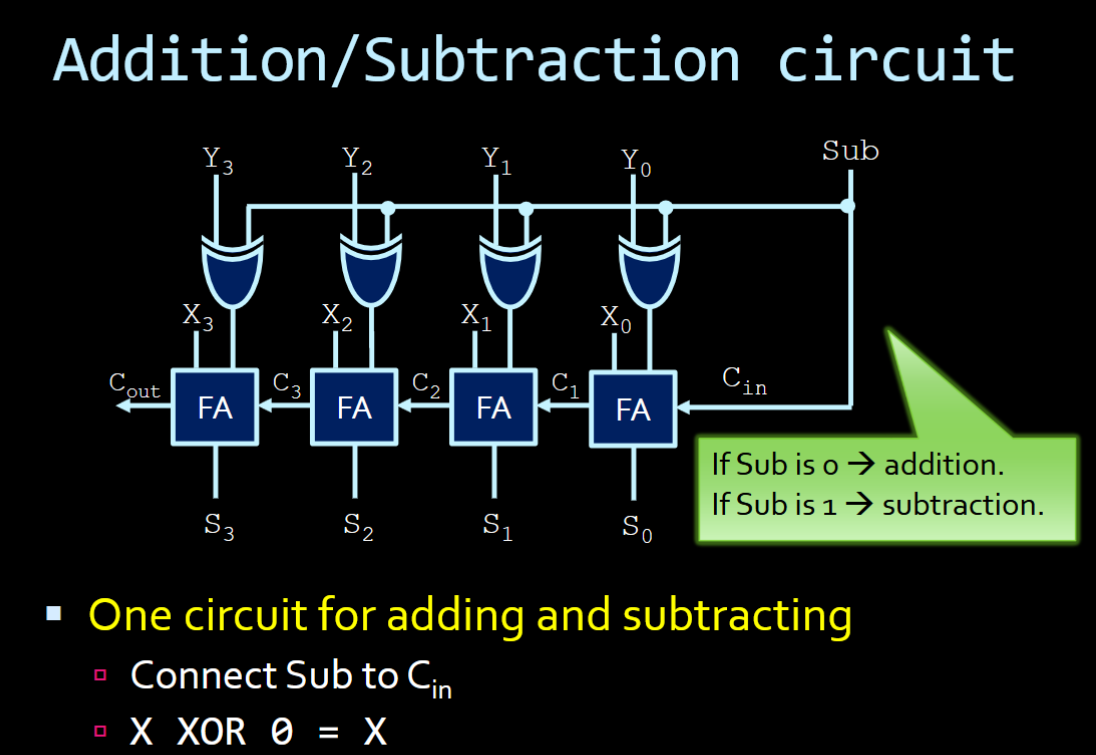
Utilizes Ripple-Carry Binary Adder and Binary Subtraction!
We have 3 inputs: X, Y, and S for sub(tract)
- if S = 0, we do regular Ripple-Carry addition. But, if S = 1, we need to get the 2’s complement of Y, which if you remember involves flipping every bit, and adding 1
| Y | S | Actual Y going into the FA |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
| Wait a minute, this is just a XOR gate! So we pass, into the input for each FA, and going into a FA. That is how you get this final circuit: |