03-12 (Graphs)

Def’n:

• An ADT
• A set of notes “V” (v for ‘vertices’) of size “N”
  • $N=|V|$
• Set of edges $E$ has size $M$
  • $M=|E|$
  • Note $|E|=N^2$ in the worst case. But technically we could have $1000$ notes but only $1$ edge, too.

Graphs store data items and their relationships.

edges = connections / relations The edges are not stored in the individual items, but you get get it from the graph

Types of graphs Type A) Directed

• There are arrows pointing to nodes. “cause and effect”
  • rain ⇒ bring an umbrella
  • A08 ⇒ A48 (prerequisites)
  • BST search ⇒ BST search (is recursive!)
  • Pacos Website ⇒ Pacos website (home button) ⇒ CMS page Type B) Undirected
• There is no arrow; a “connection” is a bi-directional connection always.
  • Person1 — Person2 (two people were in close proximity to each other)

Directed graphs are more generic / more information. Undirected graphs can be seen as a subset of directed graphs

Terminology	Purpose	Undirected Graph	Directed Graph
The Neighbourhood of a node	Represents the nodes a node is connected to.	Every neighbour (every related node) makes up the neighbourhood	Consider $u\to v$ where $u,v$ are nodes. Then: 1. $v$ is the out-neighbour of $u$ 2. $u$ is the in-neighbour of $v$ (since $v\leftarrow u$) Simply put: the out-neighbours are all the nodes that go out, and in-neighbours are all the nodes that go in to a node
The Degree of a neighbourhood	Useful for finding what has more connections (maybe whose more popular, or what works the best, etc.)	The degree is size of a neighbourhood	The out-degree is the size of the out-neighbourhood Converse is true with in-degree
Paths through a graph	Represents a sequence of notes that can be followed by the edges of a graph	$A⟷B⟷C⟷D⟷E$ is a path; you can get from D to A and A to D	$A\to B\to C\to D$ is a directed path; you can go from A to D but not backwards!
Paths that are Cycles	Could be a cause for concern while coding (you don’t want infinite loops occurring!)	At least 3 nodes that start and end with the same node: $A⟷B⟷A$	Any number of nodes that start and end with the same node: $A\to B\to A$ or even $A\to A$

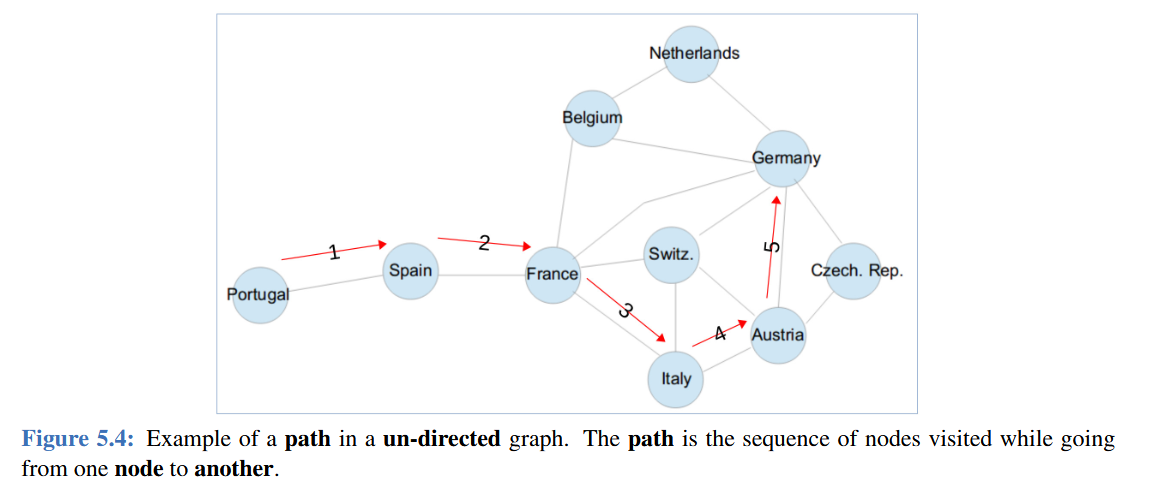A node that points to itself is in its own neighbourhood.

Graph’s are ADTs and have 5 operations

• Adding / Removing a node
• Adding / Removing an edge
• Querying an edge

There are two ways to represent graphs: Adj matrices and adj lists. These solve the two problems we face when attempting to

When creatin a graph, we need to consider two problems:

1. How to store the V (set of nodes) efficiently
   1. We can use any data structure (an array, linked list, or even a BST)
2. How to store the E (edges) efficiently 2. This is where adjacency matrices or adjacency lists come into play

Adjacency Lists

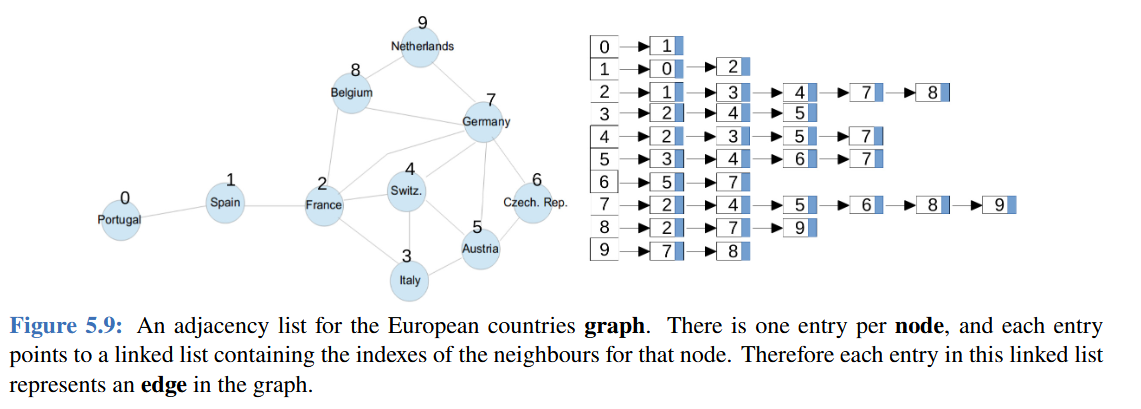
An adjacency list is an array (1 entry for each node). Each node has an associated index so we can access the actual “list” easier.

Each entry in the list contains itself a list for all the nodes the associated node is connected to.

todo is the adj list the array and the lists, or just the list???

For undirected graphs where X--Y is a connection, you would node X in the adjacency list for Y and the node Y for the adjacency list of X

Adjacency Matrices

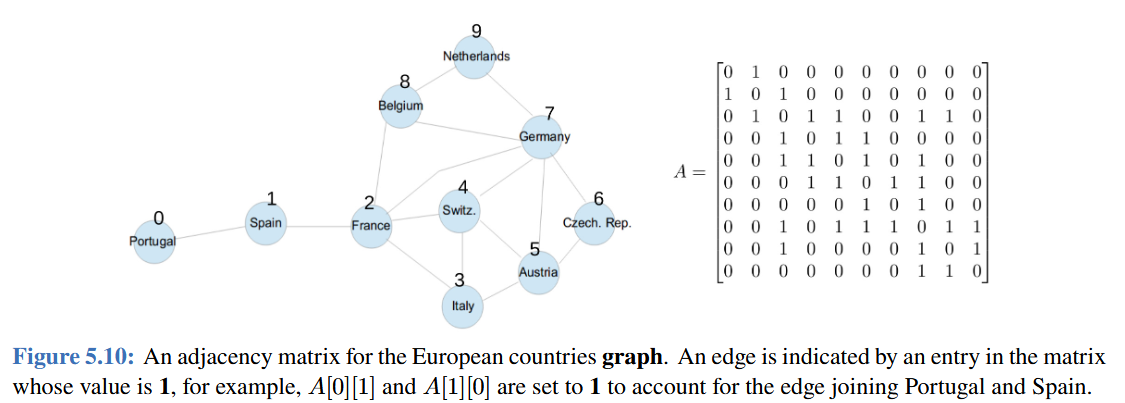Adj matrix: Similar to the list except it’s an $N\times N$ 2D array (remember $N=|V|$)

• Lowkey this is better and faster but memory is die
• Adj[i][j] = 1 $⟹$ node $i$ is related to $j$
  • ”$i$ is an in-neighbour of $j$“
• In un-directed graphs, nodes cannot point to themselves. That makes the adjacency matrix of un-directed graphs symmetric where the diagonal will always be 0’s.

todo do exercise 5.3 it seems good!

Efficiency of Adj. Lists vs Matrices

First, note that adjacency lists will be far more space efficient since the matrices are not space efficient. But otherwise the matrix has a lot of speed benefits as show in Table of Common Complexities

Operations on graphs

(you can ignore as I explain it better in Table of Common Complexities but this is for safety.)

The O(n)‘s are for worst case

The most # of edges will be (N-1)(N-2)(N-3)…(1) = G ⇒ O(n^2)

• todo why exactly (check notes)
• Update: i checked the notes and I never saw anything of the sort so I will ignore it.
• for me, $|E|=N^2$ in the worst case scenario.

1. Adding an edge (i, j) (counting # of … ?)
   1. For AL (adjacency list): Is big O(1) if we insert at the head
   2. For AM: Also O(1)
2. Removing an edge (counting # of traversals)
   1. For AL: O(n) (gotta traverse thru list)
      1. An item can be connected to at most N-1 items. Traversing to the N-1’th item will be O(n). Deleting it is 1
   2. For AM: O(1) cuz you simply index twice
3. Adding Node (counting # of nodes copied over)
   1. AL: O(n)
      1. You create a new array which takes N steps to do.
   2. AM: O(n^2)
      1. Creating a matrix would imply you copy over $N\times N$ nodes
4. Deleting a node
   1. AL: O(n^2)
      1. You go thru each entry in the list (each node) and delete the node.
      2. For funzies or lazyness we’ll just set the deleted entry in the list to NULL instead of updating the entire list
      3. Each node = N * N-1 traversals = N^2 !
   2. AM: O(n)
      1. You just zero out a row and column, which is 2N operations which is O(n) :>

Then we talked about Recursion