ALU

Does all the math (and not just adding!)

• The “arithmetic thing of a microprocessor” = ALU
  • Also does logic operations)
  • That was Lab 2
    • There is no “standard” ALU. Our lab 2 ALU is just “an” ALU but different ALUs may do different things

Summary

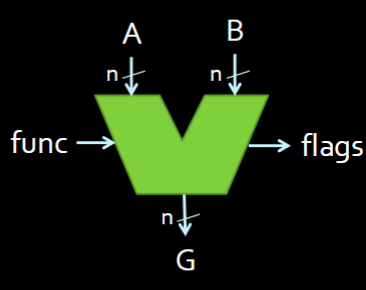
• Takes A and B inputs (of the same size $n$), a func (of varying size; should be 2 bits in our ALU from lab 2).
• Outputs G of size $n$ and ALU Flags
  • depends on your ALU

The “control unit” is what uses the flags

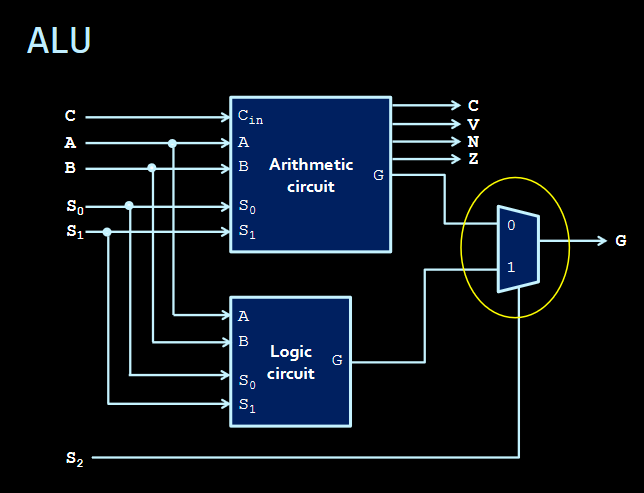
• $S_2$ chooses if you are either doing arithmetic (i.e. adding / subtracting alongside your flags) when $S_2=0$ or logical operations when $S_2=1$

n-bit ALU Block Diagram

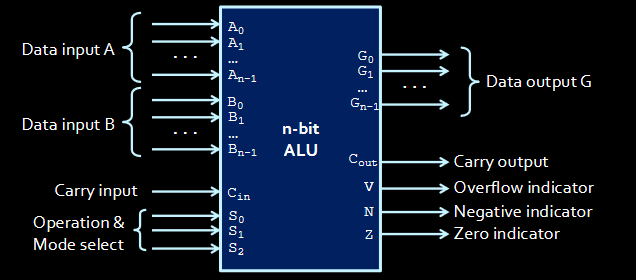
• There are n inputs for A and B as well as n outputs for G
  • todo Why not have 1 fat wire going in instead of a bunch of separate inputs? It doesn’t matter that much but it would trip me up

Making a “simple” ALU

Not a full-fledged one like a MIPS-32 ALU (that we will use after this point) Should support Arithmetic and Logical operations though

We input the 2 numbers A and B as well as S (your select bits) and $C_{in}$

• The $C_{in}$ is the same as the one for addition / subtraction. Since the ALU has an adder, we will connect $C_{in}$ to the adder
• Used for incrementing

We output G as well as VCNZ, which are 4 “flags” where each bit has its own meaning. Extra info alongside the literal results.

• V = overflow (did the addition overflow? Is the $C_{out}$ 1?)
• C = Carry out $C_{out}$
  • We will talk abt V and C later; they are different. There are times where we discard a carry out but the result is still valid (todo )
• N = result is negative (easy to make!)
• Z = if the result is zero (if the out is ALL zeros)

The A of the ALU (Arithmetic Component)

The ALU = A computer and logic to output more stuff with the computer The A = The part that adds depending on the select bitstodo is that right?

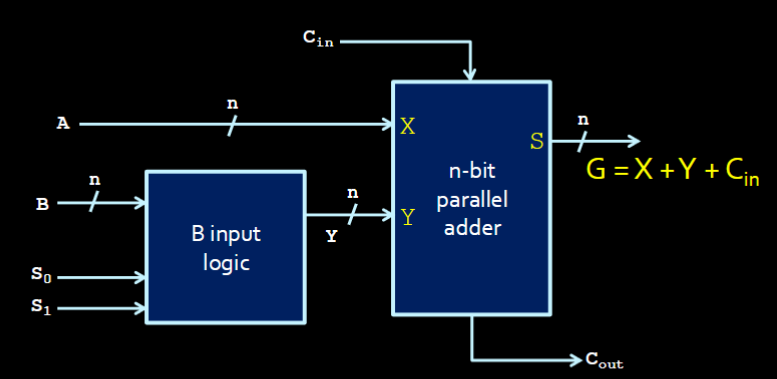Fundamentally, G = X + Y + Cin

B-input logic

• Only controls the input B (A is passed into the adder verbatim always; what B is changes what kind of operation we’re doing)
  • Similar to how, in just the adder, B was either itself, or inverted when subtracting.
  • This “B” input logic lets us do more things with B too!
• Returns Y, which is the manipulated B

The Arithmetic Component Outputs

To summarize: G is the result of this mini component. A, Y, and $C_{in}$ is what we pass into the adder to get our result. Depending on the select bits $S_0$ and $S_1$, Y will change.

Let’s assume $C_{in}=0$. These are the possible outputs of this Arithmetic Component:

• If Y = B (i.e. if sending B through “as is” means addition):
  • G = A + B
  • Addition
• If Y = 111…1 (i.e. Y = -1):
  • G = A - 1
  • Decrement
• If $Y=\bar{B}$
  • Then B is negated but NOT its negation. Remember: $-B=\bar{B}+1$ to get the 2’s complement
  • G = A - B - 1
  • Subtraction - 1
• If $Y=\mathrm{0000....0}$
  • G = A
  • Transfer As for when $C_{in}=1$, well here’s a table with all the permutations:
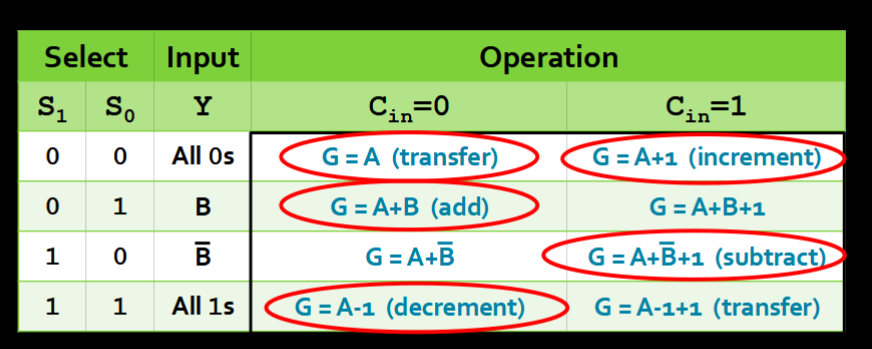
• Only 5 of them “mean” something. They are the circled ones.

The L Part of the ALU

This part returns common logical operations (in addition to the arithmetic ones from before)

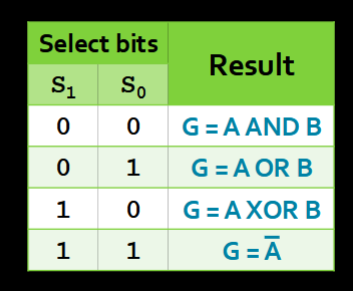
• To choose the operation depending on the select bits, we use a tried-and-true MUX!
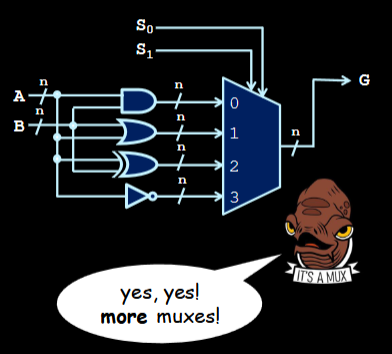
• Depending on your select bits S, we choose between the 4 logical operations and select between the operations via a MUX
  • $S_1$ and $S_0$ select between the 4 logical operations
  • $S_2$ is another bit that selects between using logic operations and arithmetic operations
  • So S really carries a lot of weight here!
    • So we have an “Arithmetic Circuit” and “Logic Circuit” with $S_2$ controlling between which two we are using.