The point of complexity ⇒ independent of implementation / abstraction #todo Just merge w/ the before notes

”The measure / meaning of Big O notation is the smallest growing function $g (n)$ such that $f (n) \leq c g (n)$ where $f (n)$ is the actual work done.” #todo this is final exam material :)))

How is it useful? It lets us compare things and compare algorithms.

When does it apply? ONLY for LARGE N’s where the N is problem dependent.

How to “do this” whatever that was

We define a unit of work
1. e.g. comparisons, checks for null, math operations, etc. etc.
2. Any 1 “operation”
3. another example: if the unit of work is “addition”,

for (int i - 9; i < 10; i++)
{
	sum = sum + 1;
}

if we choose the unit of work to be “addition” then the above would run 20 units (10 from the sum = sum + 1; 10 from the for loop’s ++ as well)

Another example

for (int i = 0; i < N; i++)
 
for (int i = 0; i < N; i++)
	for (int j = 0; j < 10; j++)
		array[i] = array[i] + j;

Unit is addition again. The above runs N + 10N + 10N + N = 22N times Uhhhh am confused now.

for (int k = 0; k < 10; k++) --> 10 times
	for (int i = 0; i < N; i++) --> N*10 times
		for (int j = 0; j < 10; j++) --> 10(N*10) times
			array[i] = array[i] + j; --> 10(N*10) times

The sum is 210N + 10

All of the above examples are 0(N) as they are all linear. So the examples are all “the same efficiency”

Common complexity classes

$O (1)$ (The smallest!) Work is constant.
1. Think of indexing an array, or inserting at the head of a linked list.
$O (l o g (N))$
$O (N)$
$O (N^{2})$
$O (N^{3})$ (oh boy)

Searching in large collections

Containers we know of so far:

Arrays
Linked lists

Worst case of finding something:

We assume the items are added in random order.
Searches happen in random order
The unit of work is the checked # of entries

The worst complexity will be $N$ Linked lists will be the same as N (you gotta traverse the whole thing — worst case)
The AVERAGE case for either the array or linked list will be N/2 (between 1 and N)
The BEST case will be O(1) when the first item is the one we want to find. Conclusion: Big O does not just represent the worst case of an algorithm.

Binary search

Precondition: the array must be sorted It is fast halving thingy yeah Worst case is $O (lo g_{2} (N))$ The average case is $O (l o g_{2} (N))$

bububbut sorting takes time!!! That is the downside of this. The cost of sorting is big. So big in fact it might negate any benefit of using bin search.

So really we would use binary if we want to search “A LOT”. So the use case is dependent on how many times you’re even gonna search.

AVG = $\sum$ # of steps to complete search $\times$ probability of the # of steps

The sum for quick search is $\sum_{k = 1}^{l o g (N)}$
With 1 step, we have 1 * 1/N (as there is a 1/N chance we get it on the first try)
With 2 steps, we have $2 * 2/ N$ because the function splits two ways
todo Look at the photo I too
It converges to $lo g_{2} (N)$

bin trees

dynamic
allows us to have a search fast fast w/o actually sorting a LL or array

But why can’t we just use a sorted LL ?

Can you do binary search on a linked list?
No, because you do not have arbitrary access to any entry; it would require a traversal
todo ask noah what he meant by random access. ll’s don’t have “random access” (?)
Now let’s consider the complexity of building this sorted linked list
- Let work be # of nodes checked. The inserting function has on average O(N/2). We have to go through all N notes.
- The cost of adding the first node is 1, the second is 2, the third is 3, etc. etc. Something about $\frac{N}{2} \times (N - 1)$
- todo WHUHUHAHWUGA (another photo taken)

We want an ADT that supports fast/efficient search, sort, delete (average case) without paying for the $0 (Nl o g (N))$ cost of sorted.

Finding 1 item to a sorted array has $O (l o g_{2} N)$ complexity. However shifting the whole array is another $O (N)$

Tree time for real

Each node has the data, and 2 children nodes. A binary tree will always have 2 children

Trees have “children”. The nodes at the bottom without any children are leaf nodes (but they can be any any level). L1 would be the top level w/ only 1 node. Each L $i$ level has $2^{i - 1}$ nodes at most.

A binary Search Tree is a binary tree with a fun BST constraint

Each node contains a “key” value
They key is unique!!! Otherwise you can’t search two nodes simultaneously.
BST constraint →
1. At any node in a BST, it must be true that if a key value is not the key at that node, THEN
  1. if the query key < node key, then query key is in the left sub-tree
  2. if the query key > node key, then query key is in the right sub-tree
  3. Think of 15 as the query and 17 is the node key. Then the sub-tree will be in the left subtree of 17

We make a BST with the numbers 4, 26, 314, 7, 14, 101, 8,2,4 The first number 5 will be the root.

26 is bigger than 5, so it goes into the right subtree of 5.
314 is bigger than 5, bigger than 26, so it goes to the right of 26
etc.etc. It’s quite simple!
todo finish the tree

Tutorial Time

bin search

Find the center item (usually n/2 is good)
if item is what we want, we done
else if the item is < what we want, we go to the bigger half
1. if the item is > what we want,,, yeah you get the idea
You do that same process in the new chunk until we’re done.

complexity yaya

big O takes the “faster” growing function. So N^2 grows faster than N.

BST = binary tree with extra characteristics

values / keys
easy to search thingys with
yes yes

Debugging:

Test cases
Using printf()
Even if a case is very difficult to reach, it is still your duty to fix it!

Tb Notes for things i should remember

Computational Complexity: A way of comparing different algorithms in terms of computational cost for carrying out a task.

We need a measure of the amount of work a algo has to do for N data items

By comparing “complexities” we can conclude an algo is faster than another for large collections Slower growing functions beat of the faster ones as data items increase

Big O notation lets us reason the efficiency of algorithms in terms of general classes of functions

Depends on the unit of work
- e.g. work could be “number of comparisons”
i.e. linear search on arrays is a class.
Big O makes explicit this slowest-growing function that characterizes these times
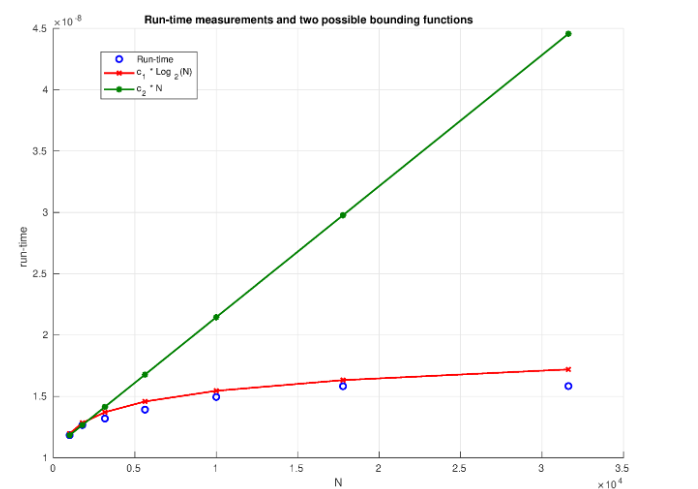
Usually $f (N)$ describes run-time. If $f (n)$ is the run-time of a binary search function, then it will check at most $lo g_{2} (N)$ entries. So we state $f (N) = O (lo g_{2} (N)) ⟹ We expect f (N) \leq c \cdot lo g_{2} (N) for a large enough N$ Different programs in different languages, if implemented correctly, will have the same Big O
Consider $f_{1} (N) = .75 \cdot N$ and $f_{2} (N) = 1.15 \cdot N + 1.12$ . These are the runtimes we found for two programs using linear search.
- Note these are both characterized by $c N + k$ where c and k are constants
We have that $f_{1} (N) \leq c \cdot N$ for a sufficiently large $N$ and some $c$ . The same goes for $f_{2} (N)$
So $f_{1} (N) = f_{2} (N) = O (N)$ as the $g (N)$ (the slowest-growing function) $= N$
We ignore constants as they are not affected by the number of data-items

We want the slowest-growing function. For binary search, technically both $f (N) = O (lo g (N))$ and $f (N) = O (N)$ satisfy the def’n of big O, but it’s not useful to use $O (N$ ) as that over-estimates the run-time by a LOT.

algo complexity and problem complexity

Algorithm Complexity: Figuring out between a bunch of algorithms which one is most efficient as size increases
Problem Complexity: The theoretical lower-limit of work for the best possible algorithm.

Finding that linear search has a complexity of $O (N)$ implies it’s not possible to find an algorithm that can do it less than $O (N)$

Bigger Big O’s = harder problems to optimize.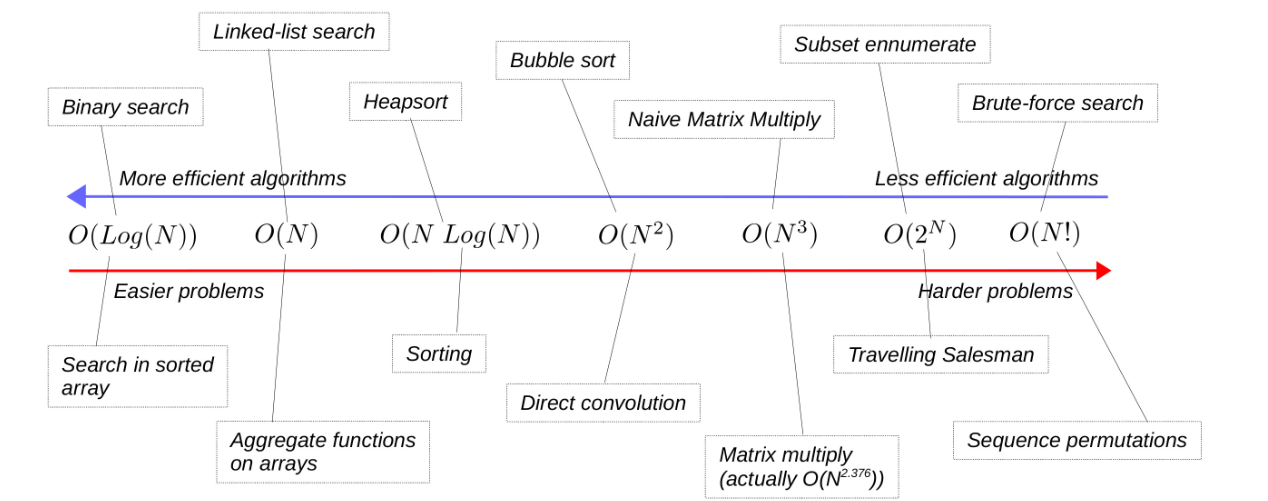

4.2

If you have a linked list, you cannot use binary search cuz you have to traverse through n/2 items and that kills efficiency. So are we stuck with sacrificing dynamism or speed?

Let’s suppose we choose speed so we stick with arrays. Then if we add an item to the array, we will need to resort it. What is the computational cost of sorting?

What is the complexity of bubble sort?

void BubbleSort(int array[], int N)
{
	// Traverse an array swapping any entries such that
	// array[i] < array[j]. Keep doing that until the
	// array is sorted (at most, N iterations of the
	// loop on i)
	int t;
	for (int i=0; i<N; i++)
	{
		for (int j=i+1; j<N; j++)
		{
			if (array[i]<array[j])
			{
				t=array[j];
				array[j]=array[i];
				array[i]=t;
			}
		}
	}
}

That first loop happens N times. For each N time, that inside loop happens N-1, then N-2, then …, then 1 time, then 0 times (when i = N, the inside loop doesn’t even run) So the number of comparisons (as that is our unit of work) is $(N - 1) + (N - 2) + \dots 2 + 1 + 0$ but we can cancel the first and last terms by adding them and noticing that the sum is always (n-1)

N-1 + 0 = N-1
N-2 + 1 = N-1
etc. So $= \frac{N}{2} (N - 1)$
as there are $N /2$ of those “pairings”

So the complexity of bubble sort is O(N^2) however that dominates the complexity of binary search… let’s try using “merge sort” instead and see what that does for us. That has a complexity of $O (N lo g (N))$ which is better but still dominates $O (lo g (N))$ .

The important detail is to consider if the data set will even change that much

If you’re making a map app, then roads and buildings won’t change super often. In that case, using this array-bin search approach might be useful since we’re searching so often!

pg 168

The actual decision on what algorithm or combination of algorithms you should use for working with a particular collection involves not only the Big O complexities for each of the components of the algorithms you’re comparing, but also the type of operations you are expecting will be carried out on the collection, and their frequency (how often they take place).

tl;dr, updating this list (by sorting it) to use binary search is NOT efficient at all. We neeeed

BSTs

Trees:

Each node has 1 or more data items which branch BSTs: These properties hold:
Data in the left tree is ⇐ the data
Data in the right tree is >= the data

Searching for an item in a BST (refer to page 35 of chapter 4)

Node* search(Node *r, int key)
{
	if (r == NULL) return NULL;
	if (r->key == key) return r;
	
	if (key < r->key)
	{
		// Go to the left cuz that has smaller numbers
		return search(r->left, key);
	}
	else
	{
		return search(r->right, key);
	}
}

To estimate the time it takes to search, we should note the work done will be at most “the height of the BST” (that being the length of the longest path from a leaf to the root)

“How many levels are there in a full BST?“todo The answer should be “it depends” (i.e. could be N to $lo g_{2} (N)$ but nothing in between)

Inserting items into a BST (refer to page 34 of chapter 4)

Node* insert(Node *r, Node *new_node)
{
	if (r == NULL) r = new_node;
	
	if (new_node->key == r->key) return r; //cannot add; already exists
	
	if (new_node->key > r->key)
	{
		// go to the right side and add it there
		r->right = insert(r->right, new_node);
	}
	else if (new_node->key < r->key)
	{
		r->left = insert(r->left, new_node);
	}
	return root; // for safety, but the above should DEFINITELY be called.
}

The code paco gave is WAY more bloated than this its honestly surprising.

The height if N items added like a linked list (i.e. the items are added in order) will be $N - 1$

“The height of a BST is defined as the length of the longest path from the root of the tree to a leaf node.” so wjat the frick why is it not N then
- Oh actually “length” implies we’re counting the “connections”. So just having a root implies the height is 0 then right?todo Should be true However if the items are added in a way that creates a complete BST then the height is given by $f l oor (lo g_{2} (N))$
I.e. if N = 7, then $l o g_{2} (N) = f l oor (2.80735492206) = 2$
For a BST to be complete, it cannot have any gaps! It’s packed with every parent node pointing to 2 nodes

The avg Big O for search / insert in a BST is $O (lo g (N))$ The setup for a BST is $O (N lo g (N))$ as for each $N$ node we insert it and that has on average $O (l o g (N))$ complexity. Any succeeding “insert” will just be $O (lo g (N))$ as well

Deletion

I talk abt this in deleting yay

Its complexity consists of finding the node to delete (on average log2(N) ) and then doing either case 1, 2 or 3. But those all have a fixed number of operations. Therefore deletion is also just $O (lo g (N))$

Traversals in BSTS

I did in 03-05 again

Anyway after all of that, we can conclude that choosing a solution depends on your use case. Note:

a) The time it takes to create a Linked list is less than a BST
b) The time it takes to make a BST is more than it takes to sorting an array in the worst case
c) BST’s and sorted arrays are faster for searching than a linked list
d) BST’s and linked-lists are more space efficient than arrays Those will help you decide.

Databases often use a mix of data structures

exercises

4.1 a) O(N^2) i think b) N + N^2 + N^2 ⇒ O(N^2) still c) No better way. it has to be N

todo

todo diff between computational complexity and big O

🪴 Quartz 4.0

Explorer

02-26 (Complexity)

Searching in large collections

Binary search

bin trees

Tree time for real

Tutorial Time

complexity yaya

Tb Notes for things i should remember

algo complexity and problem complexity

4.2

What is the complexity of bubble sort?

BSTs

Searching for an item in a BST (refer to page 35 of chapter 4)

Inserting items into a BST (refer to page 34 of chapter 4)

Deletion

Traversals in BSTS

exercises

todo

Graph View

Table of Contents

Backlinks